Erdvės ir laiko sampratos transformacija. Vartiklis

Antikos pasaulėžiūroje erdvės ir laiko koncepcija atsispindėjo Aristotelio-Ptolemėjaus kosmologinėje sistemoje, kuri buvo uždara baigtinė erdvė su Žeme centre. Ši sistema tenkino ir antropocentristinei religinei Viduramžių sampratą. Tačiau Atgimimo epochoje tapo aišku, kad ji netinka nei mokslui, nei filosofijai. Jos statiškumas, nekintamumas, baigtinumas pamažu užleido vietą naujoms savybėms: dinamika, vystymasis, judėjimas įgauna svarbiausių filosofinių kategorijų statusą. Tos sistemos griūtį pradeda N. Koperniko⁵⁾ „Apie dangaus kūnų sukimąsi“ (1543). Ir ji sudavė smūgį ne tik antropocentrizmui, nes Koperniko sistema buvo heliocentristine, bet ir teologijos pagrindams, o taip pat paaiškėjo tendencija dėl kosmoso erdvės išplėtimo.

Glaudus geocentrizmo ryšis su teologija numato griežtą kosmoso suskirstymą į du lygius: sakralinį (dangaus) ir profaniškąjį (žemiškąjį). Tuo tarpu Koperniko sistemoje santykiai tarp kosmoso objektų įgauna griežtai fizikinį pobūdį, paklusdami visuotiniams įstatymais. Kosmosas virsta konstrukcija. Ir nors Koperniko modelis taip pat yra aštuntąja sfera su joje išsidėsčiusiomis žvaigždėmis, tačiau įžvelgiamas noras „išplėsti“ erdvę: „... dangus neišmatuojamai platus lyginant su Žeme ir yra begalo didelio dydžio; mūsų jutimų atžvilgiu Žemė santykyje su danguje yra kaip taškas su kūnu, o dydžiu – kaip baigtinis su begaliniu...“ [1].

Koperniko „neišbaigtumą“ dėl erdvės tęstinumo netrukus pastebėjo ir ištaisė Dž. Bruno, pasiūlęs pasaulių daugį begalinėje erdvėje: „Aš už begalinę erdvę, ir pati gamta turi begalinę erdvę ne dėl savų matavimų ar kūniškojo tūrio dėka, o dėka pačios gamtos ir kūnų rūšių; nes dieviškasis pranašumas nepalyginai geriau pateikiamas begaliniuose individumuose, nei tuose, kurie suskaičiuojami ir baigtiniai“ [2].

Čia priminsime, kad antikos mąstytojams tai, kas už kosmoso ribų, tiesiog neegzistuoja. Atgimimo epochoje iškyla ir šis klausimas. Tad Dž. Bruno teigia, kad baigtinė Visata neišvengiamai veda prie tuštumos už jos, todėl atsisako kosmosą ribojančios sferos ir jam priskiria begalinumo savybę. Tai jis iš kosmoso atima ir kokį nors centrą, kad ir pažemindamas žmogų, atimdamas iš jo unikalumo ir reikšmingumo aureolę.

Kartu su Koperniko revoliucija keičiasi ir amžinybės samprata. Jei anksčiau pasaulio padalijimas į sakralųjį ir profaniškąjį kartu reiškė ir jo dalijimą į laiką ir amžinybę (amžinybė turėjo sakralumo statusą ir laikas ir laikrodžiai

išimtinai dieviškuoju atributu), tai dabar amžinybė tampa paties laiko savybe. Ir jei antikoje išoriniame pasaulyje teoriškai buvo galima rasti kažkokį universalų laiko matą, pvz., nejudančių žvaigždžių sferų sukimąsi, tai dabar, jau pas Bruno, bandymai matuoti laiką tampa priklausomi nuo stebėtojo, t.y. reliatyvistiniai.

G. Galilėjus, pamatęs Jupiterio ir Saturno palydovus, iš heliocentrinės sistemos atėmė paskutinius dieviškosios simetrijos likučius. Ir tada J. Kepleris atsisako „tobulų“ apskritimo formų orbitų pereidamas prie elipsinių. R. Dekartas tam tikru laipsniu materializuoja laiką geometrine išraiška, įvesdamas jį į koordinačių sistemą. Dekartas vysto absoliutaus laiko (arba amžinybės) ir santykinio laiko (matuojamo stebink kokius nors periodinius reiškinius) suvokimą: „Tačiau vienos savybės arba atributai duoti pačiuose daiktuose; kiti gi – tik mūsų mąstyme. Taip laikas, kurį mes skiriam nuo trukmės, paimtos bendrai, ir vadiname judėjimo reikšme, tėra tik žinomas būdas, kaip mes apmąstome tą trukmę [ ... ], kad apimtumėm bet kokio reiškinio trukmę vienu matu, mes paprastai naudojamės žinomų tolygių judėjimų trukme, tokiomis kaip dienos ir metai, ir taip tą trukmę, ją palyginę, vadiname laiku, nors tikrovėje tai, kad taip vadiname, yra ne kas kita, kaip būdas mąstyti apie tikrąją reiškinių trukmę“.

Labiau matematizuotoje formoje absoliutus ir santykinis laikas bei erdvė sutinkami I. Niutono koncepcijoje. Absoliutus laikas (jis ir tikrasis, matematinis) visata teka tolygiai, nepriklausomai nuo nieko, kas išoriška. Tą laiką Niutonas ir vadina trukme. Absoliuti erdvė irgi nepriklausoma nuo jokių išorinių dalykų – tai tik materialių daiktų talpykla. Yra ir santykinė erdvė – materialiųjų daiktų ilgis. Šie yra absoliučios erdvės matais. Niutonas taip apibrėžia santykinį laiką: „Santykinis, atrodantis arba įprastinis laikas yra arba tikslus, arba kintantis, pajuntamas jutimais, išorinis, atliekant kokį nors judėjimą, matas, kasdieniniame gyvenime naudojamas vietoje tikrojo matematinio laiko, toks kaip“ valanda, mėnuo, metai“ [3].
Taigi, santykiniai laikas ir erdvė yra empiriniai analogai absoliutiesiems.

Reliatyvistinę erdvės ir laiko koncepciją randame ir pas G. Leibnicą, kur ji glaudžiai susijusi su jo monadologija. Tačiau Leibnicas neigė absoliutų laiką ir erdvę – jie priklauso arba nuo kiekvienos atskiros monados suvokimo, arba suvokimų visumos: „Aš ne kartą pabrėžiau, kad laikau erdvę, kaip ir laiką, kažkuo grynai santykiniu: erdvė – egzistavimo tvarka, o laikas – nuoseklumų tvarka“ [4].

Savitą sintezę sutinkame pas I. Kantą. Erdvė nėra empirine sąvoka, kurią galima išvesti iš išorinės patirties. Be to, išorinė patirtis galima būtent įsivaizdavimo apie erdvę kaip išorinių sąmonės atžvilgiu objektų ar reiškinių dėka: „Erdvė yra būtinas apriorinis įsivaizdavimas, esantis visų išorinių suvokimų pagrindu“.
Tokiu, neišvedamu iš empirinės patirties, Kantas laiko ir laiką. Tai irgi apriorinis įsivaizdavimas. Erdvė laikas pas Kantą yra subjektyvios ir būtinos pajautimo sąlygos, kas reiškia, kad jų realumas taikytinas tik reiškinių, fenomenų pasauliui. Jie neturi santykio su noumenais, kurie yra nepažinūs ir anapus laiko.
Pirmoji Kanto antinomija: a) pasaulis turi pradžią laike ir baigtinis; b) pasaulis be pradžios laike ir begalinis. Kantas parodo, kad nė viena alternatyvų negali būti išspręsta teigiamai, o tai liudija apie Kanto įsitikinimą apie įsivaizdavimų apie erdvę ir laiką neobjektyvumą.

Hėgelis tvirtina, kad struktūros supratimas galimas tik išnagrinėjus erdvę ir laiką kaip materijos judėjimo elementus, kurių struktūra gali keistis priklausomai nuo judėjimo prigimties pasikeitimo. Judėjimu momentui „dabar“ atitinka tam tikra erdvės „atkarpa“, o ne vienas taškas: „Judėjimas patenka į Zenono antinomiją, kuri neišsprendžiama, jei izoliuojami vieta ir laikas, jei pirmoji suprantama kaip taškai erdvėje, o antras – kaip taškai laike; ir antinomijos išsprendžiama, t.y. judėjimus reikia suprasti tik taip, kad erdvė ir laikas nenutrūkstami savo viduje, ir judantis kūnas vienu metu yra vienoje ir toje pat vietoje, t.y. vienu metu randasi kitoje vietoje...“.

Kadaise žmogaus sąmonėje kilo supratimas, kad jame yra kažkas, kas neapčiuopiama, bet esantis su juo tol, kol gyvas. O gyvendamas dermėje su gamta, jis buvo įsitikinęs, kad ir ji turi sielą. Vėliau ėmė tikėti, kad turi (labai subtilų) ryšį ir su Visata – ir juo aiškino daugelį reiškinių, dabar priskiriamų parapsichologijai. O tada ir Visada turi kažkokį sielos analogą, įvairialypį, daugiamatį. Fontenelio (17 a.) „Apmąstymai apie pasaulių daugį“ ilgam užvaldė mąstytojų protus. Laikoma, kad mums žinomas ir nežinomas, pasaulis yra daugiamatis.

Vienmatė erdvė turi dvejetaines sąvokas: plius-minus, taip-ne, nulis-vienetas. G. Leibnicas 1697 m., susižavėjęs susikurtomis dvejetainių skaičių aritmetinių veiksmų taisyklėmis, laikė jas geriausiu vienintelio Dievo buvimo įrodymu. Bet ar buvo tais laikais dar su kuo lyginti nenorint pakliūti ant inkvizicijos laužo? Daugelis su ironija pažvelgė į jo nuomonę. Dž. fon Neimanas išleido „Išankstinę elektroninių skaičiavimo prietaisų loginės sandaros apžvalgą“ (1946), kurioje dvejetainiam skaičiavimui taip pat skyrė pirmenybę.

Analogiška vienmatei laiko XY koordinačių sistemą, - o pagal tą principą sudaryti natūralūs (beje, ir dirbtiniai) bipoliariniai polimerai (vandens molekulė). Kadaise R. Dekartas į aritmetiką atnešė geometriją, sumąstęs koordinačių sistemą – ir taškas virto skaičių pora, o linija – formule. To dėka Rymanas ir Lobačevskis naujai pamatė Euklido geometriją. Begalybė turi savo geometriją.

Į Dekarto „Mąstau, taigi, esu“ įdėta gili filosofinė prasmė, apibūdinanti pagrindinį žmogaus psichinės veiklos principą - cogito. Jo esmė, jei paprastai, kad tai, kas iš psichikos, egzistuoja tik mūsų sąmonėje. Materialių daiktų, išorinio pasaulio suvokimas, įsisąmoninti norai – tai psichinės realybės pasaulis. Jų visumą Dekartas vadino žinojimu, kad sąmonė egzistuoja. Anot jo, psichologija – tai mokslas apie sąmonę, apie sąmonės kaip atskiro pasaulio, kuriame realiai „verdame“, išskyrimą. Šiuolaikiniai psichologai įvedė savų pataisų, bet iš esmės nepakeitė Dekarto principų. Ten tiksliau nei sakė Z. Froidas, pagal kurį psichologija – nežinojimas, kad egzistuoja sąmonė. Jo tezėje vyrauja pasąmoniniai dalykai – „visi mes ligoniai, nes nėra ribos tarp normos ir patologijos“. Taip, bet tik klinikiniais atvejais. Gal jis pagal save sprendė?

Trimatė erdvė - tai mums pažįstamas aplinkinis pasaulus, žymimas koordinatėmis XYZ. Jo pavyzdys – DNR molekulė, su kuria, kaip ir rytdiena, aišku, kad bus, tik neaišku, kokia.
Keturmatė erdvė – trimatė su laiku: todėl ji tapo asmeniniu moterų priešu, o jos pavyzdys – mūsų besikeičiantis kūnas.

Toliau prasideda tamsus miškas, parapsichologų „teritorija“ – Nutikimų laukas, kuriame, tarsi nakties košmare, vienu metu vyksta daugybė dalykų, nepriklausomų nei nuo laiko, nei nuo masės, atstumo, greičio.

Sensorinės, penkiamatės erdvės – kažkas subtilu, sensorinių pojūčių lygmenyje (astraliniame pasaulyje: nuo „astra“ - žvaigždė). Žvaigždžių kultai, Mėnulio-Saulės mitai, budistinių Rytų idėjos apie begalinį laike ir erdvėje gyvąjį pasaulį – mėgstama senovės tema. Tarkim, Pitagoras mistinę prasmę teikė taisyklingam žvaigždėtam daugiakampiui – pentagramai. Jis jį paskelbė sveikatos simboliu ir pitagoriečių ženklu.

Asmens mentališkumas: plačiąja prasme - noosfera, siaurąja – ežiuko apmąstymai rūke, o parapsichologijoje – šešiamatė erdvė. Jos „rūkai“ prisodrinti minties formų ir vaizdinių, gebančių materializuotis į „primityvus“, t.y. daiktus. Čia išsiskiria Platonas, kuriam idėjos – amžini ir nekintami daiktų pirminiai vaizdai, o daiktai – tų idėjų atspindžiai. Vėliau išsivystė neoplatonizmas, prie kurio klijavosi Aristotelio, neopitagoriečių, Proklo ir t.t. iki pat Boecijaus³⁾ idėjos.

Sako, kad septynmatė erdvė - tai, kas mumyse, t.y. siela. O ją paminėjus, kalba nustoja būti rimta. Net teologai nesutaria, nepateikia vieningo paaiškinimo... Nors viską, bendrai paėmus, turėtų žinoti Širinskienė...

Papildomai žr. Matavimai

Dekarto koordinatės 3D Dekarto koordinatės

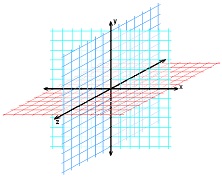
Dekarto arba stačiakampės koordinatės nurodo taško poziciją dvimatėje plokštumoje (x,y) ar trimatėje erdvėje (x,y,z) statmenų ašių atžvilgiu. Sistemą 1637 m. įvedė Renė Dekartas (1596-1650), nors keliais metais anksčiau jas panaudojo P. Ferma. Kadangi Dekartas ėmė ją plačiai naudoti, jai suteiktas Dekarto vardas. Abu naudojo vieną ašį kintamą ilgį matuojamą tos ašies atžvilgiu. Dvi koordinačių ašys 1649 m. įvestos po to, kai Fransas van Schotenas¹⁾ su savo mokiniais į lotynų kalbą išvertė Dekarto „Geometriją“. Jie, bandydami paaiškinti Dekarto idėjas, komentaruose įtraukė kelias koncepcijas.
Tačiau jau 14 a. prancūzų dvasiškis Nikola Orezmietis (apie 1320-1325 - 1382) naudojo panašias konstrukcijas.
Vėliau buvo sukurtos kitos koordinačių sistemos: poliarinės (17 a. vidurys), sferinės ir cilindrinės.

¹⁾ Fransas van Schotenas (Frans van Schooten, 1615-1660) – olandų matematikas. „Matematiniuose etiuduose“ pirmąkart išsprendė uždavinį apie duoto skaičiaus daliklių kiekį.
Nuo 1631-35 m. studijavo Leideno un-te, tada ėmė dėstyti Inžinerinėje mokykloje. Po 2 m. Leideną aplankė Dekartas ir paprašė Schoteną parengti iliustracijas jo (dar neišleistai) „Geometrijai“. Paveiktas Dekarto idėjų, apie 1639 m. parašė trumpą veikalą apie simbolinę algebrą. Kartu Dekartas davė jam kontaktų, kurie leido pradėti jam keliauti ir tobulinti matematines žinias.
1646 m. išleido F. Vieto²⁾ (1540-1603) darbus, o taip parengė ir lotynų kalba išleido Dekarto „Geometriją“ (1649) su savo komentarais, vystančiais jos idėjas. 1657 m. jis pasiūlė tas idėjas praplėsti į trimatę erdvę.

²⁾ Fransua Vietas (Francois Viete, seigneur de la Bigotiere, 1540-1603) - prancūzų teisininkas (pagal profesiją) ir matematikas, 1591 m. įvedęs simbolinius žymenis algebroje. Jis išvedė bendrą 2, 3 ir 4 laipsnio lygčių sprendimo metodą, sudarė lygties koeficientų ir šaknų sąryšių formules; su algebrinių lygčių apytikslio sprendimo metodą. Žinoma Vieto teorema – kvadratinių lygčių sprendimas netaikant diskriminanto. Jo garbei pavadintas krateris Mėnulyje.

³⁾ Boecijus (Anicius Manlius Severinus Boethius, apie 477-524) – Romos senatorius, muzikos teoretikas, teologas ir filosofas neoplatonikas. Jo „Apie muzikos mokymą“ įėjo į Viduramžių kvadrilijaus mokymo sistemą (kaip ir “Aritmetikos pagrindai”) – jame jis rėmėsi turimais graikų šaltiniais, parodančiais, kad muzika yra skaičių mokslas. Paskutiniais gyvenimo metais apkaltintas valstybės išdavimu, pateko į kalėjimą ir nuteistas mirties bausme. Laukdamas bausmės parašė svarbiausią savo veikalą „Filosofijos paguoda“ (De consolatione philosophiae), kurioje bandė suderinti asmens valios laisvę su Dievo planu. Jis aiškino, kad tai, kad Dievas žino mūsų būsimus veiksmus, tai nėra privaloma pačių tų veiksmų priežastimi. Taip pat parašė traktatų apie logiką (dialektiką) bei teologinius „Apie Trejybę“, „Apie katalikų tikėjimą“, „Prieš Euticheną ir Nestorą“ ir kt.
Skaitykite Kodėl verta skaityti Boecijų?

⁴⁾ Nikolajus Kopernikas (Mikołaj Kopernik, 1473-1543) – lenkų dvasininkas, astronomas ir matematikas, suformulavęs heliocentristinį visatos modelį, kurio centre yra Saulė (analogiškai Aristarchui Samiečiui, gyvenusiam 18 a. anksčiau). Tai išdėstė knygoje „De revolutionibus orbium coelestium“ („Apie dangaus sferų sukimąsi“, 1543), kurią rašė apie 40 m. Šiai knygai pradžioje buvo pritarta; ir tik daug vėliau, dėl Džordano Bruno interpretacijų, 1616 m. ji buvo uždrausta Bažnyčios.
1491 m. įstojo į Krokuvos universitetą, kur studijavo matematiką, vėliau klausėsi paskaitų Vokietijos ir Italijos universitetuose. Į Lenkiją grįžo 1506 m. ir 6 m. praleido Varmės Lidzbarko pilyje asmeniniu dėdės, kuris buvo vyskupu, gydytoju, o laisvalaikiu užsiimdamas astronominiais stebėjimais ir pritaikydamas matematiką planetų padėčių paskaičiavimams. Kopernikas pripažino, kad planetos juda apskritimais (o ne elipsėmis), tačiau planetų sistemos centru laikė Saulę. Tai palengvino planetų judėjimo skaičiavimus, o regimas planetų „atbulinis“ judėjimas nutinka, kai Žemė aplenkia išorines planetas. Kopernikas šią heliocentrinę sistemą pagrindė griežtai matematiškai, apibendrino idėjas trumpu rankraščiu, kurį 1530 m. išsiuntinėjo draugams.
1512 m. persikėlė į mažą Fromborko miestelį, kur atliko dvasininko pareigas. Jame pastatė hidraulinę mašiną, tiekusią vandenį į namus; kaip gydytojas padėjo 1519 m. maro metu. M. Kopernikas buvo ir medikas, diplomatas, geografas, astronomas, pinigų teoretikas ir dėdės privatus patarėjas. Parašė „Traktatą apie pinigus“. Jo kapas ilgą laiką buvo nežinomas, - ir tik 2005 m. galutinai nustatytas esant Fromborko katedroje.
Koperniką pašiepė ir protestantai. Ž. Kalvinas klausė: „Kas drįstų Koperniką iškelti virš Šventojo rašto?“ M. Liuteris sakė: „Naujasis astrologas, įrodęs, kad Žemė, o ne dangus ir dangaus skliautas juda ... kvailys, panoręs pakeisti visą astronomijos meną! Tačiau Biblijoje pasakyta, kad Jošua liepė Saulei, o ne Žemei sustoti“. Taip pat skaitykite >>>>>