Paviliota senovinio žaidimo. Vartiklis

Šiaurės Dakotos valstijos un-to matematikos doktorantę Lindsay Erickson sužavėjo senovinis nimo žaidimas Jis yra pilnos informacijos žaidimas, nes abu žaidėjai žino, ką daro jo oponentas kiekvieno žingsnio metu ir jame nėra atsitiktinumo elementų.

Šiame universitete Lindsay gavo matematikos bakalauro laipsnį 2006 m. Kaip iškili studentė, gavo NSF paramą, o taip pat kelias stipendijas daktarinei. Vieną vasarą matematiką studijavo Vengrijoje.

L. Lindsay yra nebloga nimo žaidėja, o savo darbe panaudojo grafų teoriją. Jos 60 psl. daktarinė disertacija parodo, kad įvairūs sprendimai priklauso nuo grafų struktūros. Ji panaudojo pilnuosius, dvidalius Petersono grafus, hiperkubus. Ji kiekvienai briaunai, išeinančiai iš pasirinktos viršūnės, priskyrė sveikas reikšmes, atitinkančias šūsnį akmenukų, naudojamą nimo žaidime.

Nimas - žaidimas

Nimas yra matematinis strateginis žaidimas, kuriame žaidėjai paeiliui šalina objektus iš skirtingų krūvų. Žaidėjas privalo pašalinti bent vieną objektą ir gali pašalinti bet kokį objektų kiekį iš tos pačios krūvos.

Nuo senų laikų žaidžiami keli nimo variantai. Laikoma, kad jis atsirado Kinijoje (ir primena kinų džianšizi, „akmenų nuėmimo“ žaidimą), tačiau tiksli jo kilmė nėra nustatyta. Europoje ankstyviausi žaidimo paminėjimai yra iš 16 a. Dabartinį jo pavadinimą davė Charles L. Bouton iš Harvardo, 1901 m. sukūręs pilną jo teoriją, tačiau pavadinimo nepaaiškino. Galbūt, jis yra iš vokiečių nimm, „paimti“ ar pasenusio anglų žodžio nim, reiškiančio tą patį. Verta atkreipti dėmesį, kad pasukus žodį NIM 180^o kampu gausime WIN (laimėti).

Nimas dažniausiai žaidžiamas kaip misere, t.y., pralaimi paėmęs paskutinį objektą. Bet kartais žaidžiamas taip, kad laimi tas, kuris paima paskutinį objektą (vadinamasis normalus žaidimas). Normalusis nimo žaidimas yra principinis Sprague-Grundy teoremai, teigiančiai, kad normaliame žaidimas kiekvienas objektyvus žaidimas yra ekvivalentiškas nimo krūvai, kuri garantuoja vienodą baigtį, kai žaidžiama lygiagrečiai su kitais objektyviais žaidimais.

Paprastai žaidžia du žaidėjai su trimis akmenukų krūvomis. Žaidimas matematiškai išspręstas bet kokiam pradiniam krūvų ir objektų kiekiui. Pvz., turint tris pradines krūvas su 3, 4 ir 5 objektais, pirmasis žaidėjas, žaisdamas optimaliai, laimi tiek normalųjį, tiek misere variantą. Žaidimo teorijos pagrindas yra dvejetainė krūvų objektų suma moduliu du (xor). Kombinatorinių žaidimų teorijoje ji dažnai vadinama nim- suma. Pvz., minėtu atveju 3+4+5=011+100+101=010

Normalaus žaidimo atveju laiminti strategija yra siekti, kad nim-suma kiekviename žingsnyje būtų 0. Tai visada įmanoma, jei suma prieš tai nebuvo lygi 0.

Misere žaidimo atveju reikia siekti, kad būtų paliekamas tik nelyginis skaičius krūvų, kuriose yra po 1 objektą.

Pastaba: Nimo žaidimas žaistas prancūzų „naujosios bangos“ filme „Praeiti metai Marienbade“ (1961).

Variantai

1. Vietoje bet kokio objektų pašalinimo, leidžiama pašalinti tik tam tikrą kiekį (1, 2, … k). Dažniausiai šis variantas žaidžiamas tik su viena krūva.

2. „21” yra misere žaidimas su bet kokiu žaidėjų kiekiu, kurių kiekvienas sulig kiekvienu žingsnius pasako skaičių. Kitas žaidėjas turi padidinti skaičių 1, 2 arba 3-imis, tačiau negalima viršyti 21; pralošia tas, kuris priverstas pasakyti 21.

3. Viename variante leidžiama vienodą objektų kiekį išimti iš kiekvienos krūvos.

4. Apvalusis nimas. Krūvos sudėliojamos ratu ir du žaidėjai paeiliui pašalina 1, 2 arba 3 gretimus objektus

5. Grundy variante du žaidėjai pradinę krūvą paeiliui dalija į dvi netuščias skirtingų dydžių krūvas.

Niekas nesako, kad sudėtingų matematikos klausimų negalėtų išspręstų mokyklos nebaigę mokiniai, tačiau tokių atvejų reta. Tačiau 2025 m. matematikos elitas liko išsižiojęs, priblokštas ir priverstas į savo ratą priimti, galbūt, naują talentą – 4-is dešimtmečius jį erzinančią problemą išsprendė 17-metė Hana Kairo¹⁾, prieš tai matematikos besimokiusi netradiciškai - izoliacijoje ir nuotoliu.

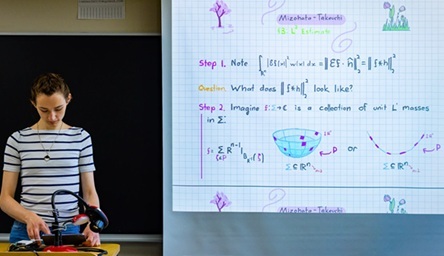Hana Kairo gimė ir augo Bahamuose, Nasau mieste. Čia ji, kaip ir jos du broliai, nelankė mokyklos ir mokėsi namuose. Ji pradėjo mokytis matematikos Khano akademijos internetinių pamokų. Vėliau pradėjo „virškinti“ viską, ką rasdavo internete. Tėvai surado pora matematikų, mokiusių nuotoliu, bet daugiausia ji mokėsi savarankiškai. Jai matematika buvo atsiveriantis platus pasaulis, skirtingas nuo jos realaus. 2021 m. per Covid-19 m. šeima apsigyveno Čikagoje senelių namuose, o ji prisijungė prie Čikagos matematikos būrelio. Įgyta patirtis leido jai pateikti paraišką 2 sav. trukmės matematikos būrelio Berklio internetinei vasaros programai, skirtai ugdyti matematikos talentus. Jai tada buvo 14 m. Vis tik gauta padrika patirtis jos dar neįtikino, kad turi išskirtinių gabumų – ji visada buvo viena ir vieninteliu atskaitos tašku palyginimui tebuvo ji pati.

2023 m., po antros vasaros Berklio būrelyje, ji svarstė apie tolimesnį savo kelią. Buvo pateikusi paraiškas į kelis universitetus, kurių dauguma ją atmetė, nes nebuvo baigusi vidurinės mokyklos. Bet priėmė Kalifornijos un-tas Deivise. Bet ar nebandyti kitur? Ir Z. Stankova iš Berklio ratelio paskatino ją dalyvauti Berklio lygiagrečioje studijų programoje ir lankyti magistrantūros lygio matematikos kursus. Šeima rudenį persikėlė į Deivisą, esantį 90 km nuo Berklio, į kurį važinėjo antradieniais ir ketvirtadieniais, o pavasarį – jau visas 5 dienas per savaitę.

2024-25 m. mokslo metams jos dėmesį patraukė Furjė apribojimų kursas aspirantams, kurį vedė prof. Ruixiang Zhang’as²⁾. Po kelių savaičių ji susidūrė su problema, apie kurią nesiliovė galvoti. Tai buvo Mizohata-Takeuči teiginio supaprastinta versija. Ją į namų užduotis (protui pramankštinti) įtraukė R. Čžanas. Ji išsprendė užduotį ir sutiko pratęsti apmąstymus.

Mizohata-Takeuči teiginys yra iš harmoninių eilučių analizės, srities, nagrinėjančios, kaip funkcijos susidaro iš banguojančių komponentų. Bet kurią funkciją galima užrašyti kaip paprastesnių bangų pavidalo sudedamųjų, vadinamų sinusoidinėmis bangomis, sumą. Kiekviena iš šių sinusoidinių bangų turi savo dažnį. Matematikai dažnai nori suprasti funkcijų, kurias galima sudaryti tik iš tam tikrų dažnių, prigimtį - tad leidžiami tik tie dažniai, kurie tenkina lygtis, kurios raižo po konkrečius paviršius, pvz., sferą. Taip yra todėl, kad funkcijos, apibrėžiančios daugelį fizinių bangų, pvz., šviesą, garsą ir kvantines daleles, yra apribotos tokio tipo dažniais.

Mizohata-Takeuči hipotezė nagrinėja funkcijas, sudarytas iš bangų, kurių dažniai randasi tokiame paviršiuje. Ir ji teigia, kad funkcijos energija (jos dydžio matas) gali būti paskirstyta ir sukoncentruota tik tam tikrose srityse. Tai tarsi leisti muziką keistos formos kambaryje. Kartais muzika atsikartos aidu, o kartais ji labai pagarsės – tačiau tai vyks tik tam tikrose vietose.

Per 4-is dešimtmečius matematikai tik nežymiai pasistūmėjo nagrinėdami atskirus hipotezės atvejus – o bendras atvejis buvo likęs atviru. Atrodė, kad jo negalima išspręsti naudojant jokį standartinį metodą. Tas neįveikiamumas kai kuriems matematikams pasėjo abejonę, kad gal teiginys ir klaidingas; tačiau kiti manė, kad jo elegantiškumas tik sustiprino teisingumo tikimybę. Bet kuriuo atveju buvo prieita aklavietė.

H. Kairo atveju abejonės buvo dar stipresnės – ji buvo naujoke šioje srityje. Jai nesisekė, ir ji nebuvo tikra, ar eina teisinga kryptimi. Nežinojo ir R. Čžanas. Bet ji skaitė ir mąstė. Galiausiai jai pavyko sukonstruoti keistą, sudėtingą funkciją iš bangų, kurios visi dažniai randasi iškraipytame paviršiuje. Paprastai, sudedant tokias bangas, jos interferuoja, neutralizuodamos arba sustiprindamos viena kitą. Tačiau pasirodė, kad Kairo funkcija neveikia, kaip tikėtasi. Jos interferencija sukūrė „marginius“, kuriuose funkcijos energija pasklido po kai kurias sritis, o kitose susikaupė fraktaliniu principu – o tai neleistina pagal Mizohata-Takeuči hipotezę. Taigi, tokios funkcijos neturėtų būti!!!

Iš pradžių jai kilo įtarimas, kad kažkas čia ne taip. Bet ji suprato, kaip gali savo griozdišką funkciją pakeisti paprastesne – ir gauti tokį pat rezultatą. Ir įtikino save (ir R. Čžaną), kad rezultatas teisingas. Ir ji paskelbę preprintą arxiv.org serveryje. Rezultatas ir netikėtas naujo autoriaus pasirodymas apstulbino bendruomenę. Rezultatas paneigia įprastą matematikų intuiciją apie tai, ką funkcijos gali, o ko negali atlikti. Dabar harmoninių eilučių analizėje teks atsižvelgti į pasikeitusią aplinką ir kyla daug naujų klausimų, nes rezultatas panaikina vieną iš perspektyviausių sąsajų tarp skirtingų harmoninių eilučių analizės dalių.

O pati Hana apsisprendė iš karto stoti į magistrantūros studijas praleisdama kolegiją (ir vidurinės mokyklos diplomą) – ir pateikė paraiškas į 10-mt programų (6-ios atmetė dėl vidurinės mokyklos diplomo neturėjimo), dvi priėmė, bet vėliau aukštesni vadovai atšaukė – ir tik Merilendo ir Džonso Hopkinso universitetai sutiko priimti ją iš karto. Ji pasirinko Merilendą...

¹⁾ Hana Kairo (Hannah Mira Cairo, g. 2007 m.) - amerikiečių matematikė, sulaukusi pripažinimo būdama vos 17-os (visai kaip E. Galua) paneigdama Mizohata-Takeuči teiginį iš harmoninių eilučių analizės. Per COVID-19 pandemiją nuotoliniu būdu dalyvavo Berklio matematiniame būrelyje. Persikėlusi į JAV tęsė studijas Kalifornijos un-te Berklyje, kur klausė ir matematiko R. Zhang’o paskaitų. Jis davė jai patyrinėti 40 m. neišspręstą Mizohata-Takeuči teiginį – ir vietoje jo įrodymo, ji surado jį paneigiantį kontr-pavyzdį. Preprintą paskelbė 2025 m. vasario 10 d.

²⁾ Ruiksianas Čžanas (Ruixiang Zhang) - kinų kilmės amerikiečių matematikas, Kalifornijos un-to Berklyje profesorius. Jo indėliu į matematiką yra svarbaus teiginio Vinogradovo vidurkio teoremoje apibendrinimas, naujų metodų naudojimas sprendžiant Karlesono uždavinį apie Šriodingerio lygties taškinį konvergavimą bei Sogge hipotezės bangų lygtims dvimačio atvejo sprendimas.

Dievas nežaidžia kauliukais?

Dantės „Dieviškoje komedijoje“ yra eilutės, skirtos azartiniams žaidimams:

Užbaigęs žaidimą trimis kauliukais,
Pralošęs nerimsta ir vėl griebia juos;
Ir mėto vienas paniręs liūdesy...

Aprašinėdamas gana įprastą tiems laikams situaciją, autorius nė neįtarė, kad ateityje žaidimu kauliukais^*) rimtai susidomės matematikai. Šio epizodo nepraleido vienas pirmųjų „Dieviškosios komedijos“ komentatorių, 14 a. italų istorikas Benvenuto da Imola, paskaičiavęs galimų iškritimų kiekį, kai metami trys kauliukai – 56.

Tačiau jis nebuvo pirmasis, išsprendęs šį kombinatorikos uždavinį. Dar 10 a. tai paskaičiavo prancūzų vyskupas Kambrė Viboldas (971–972), kuris kažkur apie 965-us, norėdamas atpratinti vienuolius nuo azartinių žaidimų ir Kauliukai gražinti juos į doros kelią, sugalvojo žaidimą (Ludus Clericalis), kuriame kiekviena iškritusi trijų kauliukų kombinacija reiškia tam tikrą krikščionišką gerą darbą. Laimėjusiam reikėjo likusiems vienuoliams įteigti atlikti tuos gerus darbus. Viboldas nustatė, kad galimi 56 variantai.
Tokį rezultatą 1523 m. gavo ir italų matematikas Nikolo Tartalja, apibendrinęs uždavinį bet kuriam kauliukų skaičiui.

Deja, jie visi klydo, nes buvo imamas tik iškritusių taškų kiekis ir neatsižvelgiama į jų tvarką. Tada vieno trejeto galimybių yra ne 20, o 120. Pirmasis apie perstatas susivokė italas Džerolamo Kardano, pats būdamas užkietėjusiu žaidėju, gaudamas 6+30x3+20x6=216 galimų rezultatų. O paprasčiausią sprendimą pasiūlė Galileo Galilėjus: išmetus vieną kauliuką gali atsiversti bet kuris iš 6-ių šonų. Tada visų trijų kauliukų visos galimos konbinacijos lygios 6³=216.

Beje, perstatų neįvertinimas ne kartą ne kartą „pakišo koją“ sprendžiant kombinatorinius uždavinius. Žinomiausias pavyzdys yra iš 18 a. vidurio, kai Ž. d‘Alamberas neteisingai paskaičiavo bent vieno „herbo“ iškritimo tikimybę metant tris monetas vietoje 8 galimų rezultatų tepaėmęs tik 4.

^*) Žaidimas kauliukais buvo labai populiarus tarp romėnų, kurie jį vadino Tesserae. TačiauRomos istorikas Katonas Vyresnysis laikė, kad žaidimas kauliukais labiau tinkamas vyresniems, nes jaunimas turėtų daugiau būti lauke lavindamas kūnus.

^**) Benvenuto Rambaldi da Imola (apie 1320-1388) – italų mokslininkas ir istorikas, mokęs Bolonijoje ir geriausiai žinomas komentarais Dantės „Dieviškajai komedijai“. Taip pat jis parengė 10-ies knygų Romos istorijos išdėstymą („Romuleon“), apie Romos imperatorius („Augustalis libellus“), parašė komentarų Vergilijaus ir Lukiano kūriniams.

John Conway¹⁾ sukurta „Topswops“ dėlionė yra tokia: imame atsitiktinai nuo 1 iki n sunumeruotą kortų kaladę. Nuimkite juo jos kortų kiekį, kurį nurodo viršutinė korta, ir tas kortas perkelkite į apačią. Tada vėl ir vėl kartokite tą patį – tol, kol viršuje atsiras korta su numeriu 1. Reikia surasti minimalų ir maksimalų žingsnių skaičių priklausomai nuo pasirinkto n.

Kadaise D. Knutas eksponentinę viršutinę ribą ir teigė, kad tai gali būti įrodyta apatinei ribai. Tačiau dabar Dr. Hal Sudborough ir Dr. Linda Morales įrodė, kad apatinė riba yra gerokai geresnė, nei spėjo D. Knutas, kuris jų įrodymą pavadino „elegantišku“ ir „žaviu“.

Halas pacitavo ilgametį „Scientific American“ skyrelio vedėją Martin Gardner‘į: „Nelaikykime Conway kortų žaidimų trivialiais. Jie priklauso perstatų aibių teorijai ir ne tik verčia įrodyti giliaprasmes teoremas, bet atsiliepia ir praktiniams uždaviniams, kylančiais, kaip atrodytų, nesusijusiose srityse“.

Įrodymas pateikiamas „Theoretical Computer Science“ 2010 m. spalio mėn. numerio straipsnyje „A Quadratic Lower Bound for Topswops“.

Martin Gardner'io knygoje „Time travel and other mathematical bewikderments“ aprašo eilė kortų dėlionių, priskiriamų J.H. Conway.

¹⁾ Džonas Konvėjus (John Horton Conway, 1937-2020) – anglų matematikas, aktyviai dirbantis baigtinių grupių, mazgų teorijos, skaičių teorijos, kombinatorinės žaidimų teorijos ir kodavimo teorijos srityse. Taip pat jis prisidėjo prie daugelio matematikos taikymų laisvalaikiui, iš kurių pažymėtinas ląstelinio automato, pavadinto „Gyvybė“ (žr. >>>>>), bei „Ūglių“ (Sprouts) žaidimo sukūrimas. Išrado naują siurrealių skaičių sistemą, kuri tapo D. Knuto matematinio romano tema. Be to sukūrė Pasaulio pabaigos dienos algoritmą. Nuo 1986 m. dirbo Prinstono un-te (užėmė Dž. fon Neumano katedrą). Žaidimą „Life“ sukūrė 1970 m.; ir kai jį M. Gardneris pristatė „Scientific American“, jis iniciavo šimtų programų, interneto svetainių ir straipsnių pasirodymą. Dabar žinima, kad „Life“ yra pilnas pagal Tiuringą (t.y. juo galima realizuoti bet kurią paskaičiuojamą funkciją). Pat Konvėjus pyko ant jo, nes laikė, kad žaidimas užgošė svarbesnius jo darbus, pvz, grupių teorijoje jis kartu su S. Nortonu suformulavo monstriškų nesąmonienų teiginius, o mazgų teorijoje įvedė naują invariantą (Konvėjaus polinomą); 2006 m. teorinės fizikos srityje įrodė laisvos valios teoremą ir t.t. Mirė nuo Covid-19.

Jau 50 m. matematikai grumiasi su vadinamąja „fiksuoto taško“ teorema. 2008 m. buvo paskelbtas beveik 30 psl. apimantis ir labai techninis straipsnis, nepaprastai priartėjęs prie jos įrodymo.

Padėkime akmenuką Katedros aikštėje Vilniuje, savo kieme ar ant palangės – ir visada žemėlapyje galėsite nurodyti tikslią vietą, kuriame jis turėtų būti. Akivaizdu, ar ne? Tačiau ne matematikams. Jie nuo 1963 m. negali susitvarkyti su vadinamąja (nors kiek ir sudėtingesne) „fiksuoto taško teorema“, kurią suformulavo Barry Edward Johnson (beje, ją bandęs įrodyti iki pat savo mirties 2002 m.). Tačiau EPFL (Ecole Polytechnique Federale de Lausanne), Lozanoje (Šveicarija) matematikų grupė rado elegantišką, viename puslapyje išdėstomą, sprendimą, atveriantį naujas perspektyvas fizikoje ir ekonomikoje. Jie tai pasiekė, kitaip ėmėsi spręsti uždavinį.

Įdomu, kad teorema pritaikoma įvairiausiems žemėlapiams, nuo planų iki metro schemų bei erdvių pavaizdavimo kvantinėje mechanikoje. Tačiau jos įrodymui yra būtina rasti fiksuotą tašką kiekvienu konkrečiu atveju. Kadangi galimų žemėlapių aibė yra begalinė, matematikai ieškojo universalaus metodo. Tai buvo panašu į svorio centro bet kokiame kūne paieškas. Ir tas taškas buvo surandamas, tačiau ... kitoje erdvėje, nei pradinė. Ir tai leido įrodyti teoremą
(žr. originalų straipsnį >>>>).