Diagramos, pakeitusios pasaulį
Įprasta sakyti, kad piešinys vertas tūkstančio žodžių. Tačiau moksle diagrama gali apibūdinti dalykus, išeidama anapus žodžių sferos. Paprastas vaizdas gali atskleisti esmę, kuri slepiasi po žodžiais ir formulėmis.
Teisingai nubrėžtas piešinys gali visiškai pakeisti pasaulio matymą. Diagrama yra daugiau nei vien fizinis atvaizdavimas to, ką matome savo akimis. Neretai reikia pašalinti informaciją, kad pabrėžtume, kas yra svarbiausia. Kitais atvejais mokslinė idėja transformuojama į vizualinę kalbą, kur esmę perprasti padeda geometrija.

Kopernikas neabejotinai suprato gero piešinio galią. Jo De Revolutionibus Orbium Coelestium (1543) heliocentrinė teorija aiškinama 405-iuose puslapiuose, kur dėstoma žodžiais, skaičiais ir formulėmis. Tačiau knygos pradžioje pateikta diagrama vienu ypu akivaizdžiai perteikia jo revoliucinę idėją: centre yra Saulė, o ne Žemė.
Jo piešinys apima kelis esminius geros diagramos principus. Koncentriniai apskritimai nėra skirti tikslioms planetų orbitoms pavaizduoti. Kopernikas žinojo, kad jos nėra koncentrinės. Vienodi atstumai tarp apskritimų nenusako, kaip toli viena nuo kitos nutolusios planetos. Tas piešinys leidžia mums suvokti paprastą, tačiau pribloškiančią idėją, kad mes nesame pasaulio centre. Tas piešinys pakeitė požiūrį į mūsų vietą pasaulyje.
Tačiau kai kurios diagramos leidžia daugiau, nei vien išgrynina sudėtingos sistemos esmę. Diagrama gali sukurti visai naują vizualinę kalbą mokslinės idėjos supratimui. Pavyzdžiui, Niutono optikos diagramos transformuoja šviesą į geometrijos kalbą. Vaizduodamas šviesą linijomis, Niutonas galėjo panaudoti geometrijos teoremas, kad nuspėtų šviesos elgseną. Tai buvo revoliucinė idėja. Pasižvalgykime į šviesas, kuros apsviečia pasaulį aplink mus. Čia nėra jokių tiesių.
O kartais diagrama lemiamas veiksnys, įgalintis patikėti žmones tuo, kas, atrodytų, yra neįmanoma. Matematikai ilgai kankinosi su kvadratinės šaknies iš -1 idėja. Skaičių tiesėje nebuvo vietos, kur šią reikšmę būtų galima patalpinti. Bet, visi suprato, kad jei toks skaičius egzistuotų, jis daug ką pakeistų matematikoje.
19 a. pradžioje trys matematikai, nepriklausomai vienas nuo kito nubrėžė piešinį, kuris tam skaičiui davė gyvenimą. Jie pateikė dvimatį skaičių išdėstymą, kuriame žinomi ir realūs skaičiai buvo horizontaliojoje ašyje, o nauji menami skaičiai (kaip kvadratinė šaknis iš -1) plėtėsi vertikaliai. Argando diagrama (pagal vieną iš autorių) padėjo matematikams patikėti tais naujais skaičiais. Ir ne tik diagrama buvo galinga
priemonė, leidžianti manipuliuoti tais skaičiais, nes jų geometrija atspindėjo algebrą, kurią tie skaičiai išreiškė. Taip gimė kompleksinių skaičių teorija.
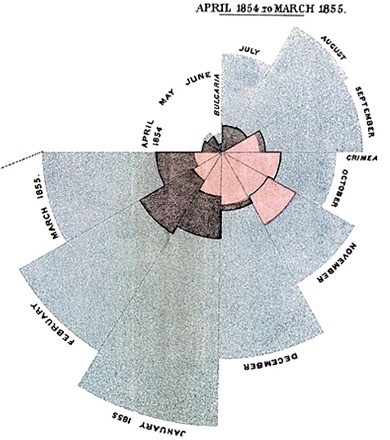
Vienas galingiausių diagramų panaudojimų yra duomenų vizualizavimas. Kai gyvename amžiuje, kuris gamina neapsakomą skaitinės informacijos kiekį, parodyti esmę tuose skaičiuose yra nepaprastai svarbu. Vienaa pirmųjų panaudojusi vizualias priemones navigacijai po skaičius buvo Florencija Naitingalė*) (Florence Nightingale, 1820-1910). Nors labiau žinoma savo indėliu slaugai, didžiausi pasiekimai buvo matematikoje. Ji pirmoji panaudojo skritulinę diagramą duomenų pavaizdavimui.
Florencija nustatė, kad dauguma mirčių Kryme yra dėl blogos sanitarinės būklės, o ne dėl žuvimų mūšiuose. Ji norėjo įtikinti vyriausybę, kad reikia pakelti higienos lygį ligoninėse. Ir kai skaičiai buvo perteikti diagrama, į ją neatsižvelgti buvo negalima. Tokia diagrama tikrai buvo verta tūkstančių skaičių (o gal ir gyvybių).
Labai svarbu, kad diagramos yra anapus žodžių. Jas suprasti gali visame pasaulyje, kalbantys bet kokia kalba. Ir būtent todėl, 1972 m. paleidžiant pirmąjį zondą, kuris turėjo palikti Saulės sistemos ribas, mokslininkai nusprendė, kad piešinys labiausiai tinka perduodant žinutę galimoms nežemiškoms civilizacijoms. Neabejotinai, jis labiau tinka kaip labas kosmoso broliams (taip pat skaitykite >>>>>).

F. Dreiko ir K. Sagano piešinyje:
- Nuogų vyro ir moters atvaizdai rodo, kaip atrodo mūsiškės gyvybės formos;
- Pioneer zondo, startavusio iš 3-sios planetos, vaizdas turi nurodyti mūsų vietą Saulės sistemoje;
- Skaičiai, perteikiami dvejetaine sistema, nusako planetų atstumą nuo Saulės (dvejetainė sistema universalesnė, nes kitos civilizacijos gali naudotis kitokia nei dešimtainė skaičiavimo sistema);
- Žvaigždėlapis nurodo Saulės vietą. Linijos nurodo pulsarus, o dvejetainis skaičius apibrėžia dažnį;
- Nurodomas mato vienetas. Apskritimas reiškia vandenilio atomą. Aplink jį besisukančiam elektronui pakeičiant būseną, išspinduliuojama banga, kurios dažnis 1,420 MHz, o ilgis 21 cm. Tai mato vienetai, naudojami diagramoje;
- Pioneer zondo vaizdas gali padėti nežemiečiams sužinoti, kokio dydžio yra žmonės (lyginant su zondo dydžiu);
- Moters ūgis parašytas dvejetainėje sistemoje: 1000 mato vienetų. 1000 yra 8, užrašyti dvejetaine sistema, tad moters ūgis yra 8 x 21cm = 168 cm>
*) Florencija Naitingalė (Florence Nightingale, 1820-1910) Anglijos visuomenės veikėja, ligoninės slaugė (šiuolaikinės slaugos pradininkė), statistikė. Ji buvo socialinės statistikos pradininko A. Ketlės gerbėja ir išleido 800 psl. knygą Apie britų armijos ligoninių valdymą (1858), kurioje buvo statistikai skirtas skyrius, kuriame panaudotos diagramos. Ji sukūrė apvalias diagramas (angl. polar area diagram), kurias vadino gaidžio skiauterėmis ir panaudojo iliustracijai, kiek buvo mirčių Krymo kare, kurių buvo galima išvengti. Nemažai jos diagramų buvo įtraukta į komisijos apie sveikatą armijoje ataskaitą. Naitingalė tas diagramas parlamente paskleidė pamfleto forma. Kaip rezultatas buvo atliktos reformos sveikatos apsaugoje ir organizuotas medicininės statistikos rinkimas kariuomenėje.
Feinmano diagramos
Trikampiai skaičiai
Matematikos keliu
Gyvenimo gėlelė
Smeilo paradoksas
Kaip supakuoti standžiau?
Surasta trilijonas trikampių
Nauji picos pjaustymo būdai
Apie Tarskio skritulio kvadratinimą
Nėra paprastos visuotinės teorijos!
Kaip išgyventi aukštesnius matavimus?
Pinavija: matematika prieš eismo spūstis
Mazgų teorija: juostos-nuopjovos teiginys
Džordžas Birkhofas: matematikas ir meno matuotojas
Klasikinės neišsprendžiamos geometrinės konstrukcijos
Semantinės derybos: Dviprasmybių modeliavimas
Egzotiškosios hipersferos: problema išspręsta
Omaras Chajamas: ne vien Rubijatai
Geriausios alternatyvos parinkimas
V. Nalimovas. Skaičiaus filosofija
Da Vinči matematinė klaidelė
Revoliucija mazgų teorijoje
Nepaprasti Visatos skaičiai
Paviliota senovinio žaidimo
Pirmasis Einšteino įrodymas
Monte-Karlo metodas
Matematiniai anekdotai
Dalyba iš nulio
Ferma taškas
Topologija
Matroidai
Vartiklis