Izingo modelis
Izingo modelis - statistinės fizikos matematinis modelis, skirtas medžiagos įmagnetinimo proceso paaiškinimui. Jį 1924 m. (vienmačiam atvejui) išsprendė vokiečių Ernstas Izingas (1900-1998). Dvimatis atvejis gerokai sud4tingesnis ir buvo įveiktas L. Onsagerio tik 1944-ais. 4-o ir aukštesnių matavimų atvejais jis aprašomas savaime susiderinančio lauko terminais. DWave Sys sukurtas kvantinis kompiuteris pagrįstas Izingo modeliu.
Modelyje magnetinį sukinį turinčios dalelės yra patalpinamos į apibendrinto grafo viršūnes. Bendru atveju grafo struktūra gali būti įvairi, bet įprastu atveju apsiribojama įvairių dimensijų gardelėmis. Modelinės sistemos elgesys yra stebimas esant įvairioms temperatūroms ir yra ieškoma fazinio virsmo taško. Taigi pagrindinė šio modelio problema ir tikslas yra supaprastinto fazinio virsmo modeliuojamoje struktūroje atkūrimas. Pastebėsime, kad šis modelis puikiai tinka ne tik įprastiems taikymams statistinėje fizikoje, bet ir turi tarpdisciplininių taikymų.Izingo modelis yra ypatingai įdomus dėl to, kad veikiausiai buvo pirmasis modelis, kuriame iš visiškos netvarkos galėjo atsirasti tvarka struktūros. Apie 20 a. vidurį vis daugiau fizikų ėmė pastebėti negyvosiose sistemose spontaniškai besiformuojančias struktūras, kurios buvo kažkas naujo, neegzistavusio atskirų dalelių suvokimo lygmenyje, o spontaniškai atsirandančio dėl sudėtingų netiesinių sąveikų tarp dalelių.
Klasikiniu pavyzdžiu yra Belousovo-Žabotinskio reakcija: į indą pilamos cheminės medžiagos (reagentai), kurie tarpusavyje ne tik maišosi, bet ir reaguoja. O tolesnėse reakcijose jau dalyvauja ne vien pradinės medžiagos, bet ir ankstesnių reakcijų produktai. Dėl to, kad dalis medžiagų, esančių šiame mišinyje, turi skirtingas spalvas,
indas ima dažytis pačiomis įvairiausiomis spalvomis taip suformuodamas struktūras laike.
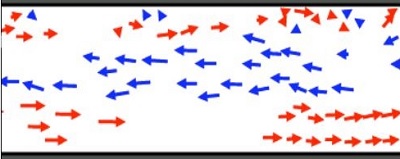
Tokius pat reiškinius galime stebėti ir gyvose sistemose. Pvz., rudenį pažvelgę į dangų pamatysime kaip paukščių būriai ruošiasi skristi į pietus. Būriui kiekvienas kiekvienas atskiras paukštis juda padrikai, tačiau būrys išlieka vieningas ir juda kryptingai. Bet rudens laukti nereikia bet kuriuo metų laiku pakankamai judrioje pėsčiųjų gatvėje galime stebėti kaip spontaniškai susiformuoja viena kryptimi judančių žmonių juostos.
Struktūros atsiranda ir mums bendraujant, formuojant socialinius ryšius. Dar praeitame amžiuje buvo suprasta, kad žmonių tarpusavio ryšius galima atvaizduoti kaip grafą. Ir visi suvokiam, kad yra daug žmonių, kurie socialiniame tinkle turi mažai ryšių, bet yra žymiai daugiau, nei galima būtų tikėtis, žmonių, kurie turi labai daug ryšių.
Struktūros spontaniškai formuojasi ir ekonomikoje - pvz., finansų rinkose didelio aktyvumo (kainų kitimo) periodai keičia žemo aktyvumo (kainų kitimo) periodus.
Modelio apibrėžimas
Kiekvienai kristalinės gardelės (vienmatei, dvimatei ar trimatei) viršūnei priskiriamas skaičius 1 arba -1, kuris vadinamas spinu (sukiniu). Kiekvienam iš 2N spinų išsidėstymo galimų variantų (N - gardelės atomų kiekis) priskiriama energija, gaunama iš gretimų atomų spinų poliarinės sąveikos:
kur J - sąveikos energija. Kartais nagrinėjamas ir išorinis laukas h, kuris dažnai laikomas silpnu:
Tada duotai atvirkštinei temperatūrai b = 1 / kBT gautoje konfigūracijoje nagrinėjamas Gibso pasiskirstymas: konfigūracijos tikimybė yra laikoma proporcionalia e-bE(S) - nagrinėjant tokio pasiskirstymo elgesį esant dideliems N.
Matroidai
Perkoliacija
Pirminiai skaičiai
Nešo pusiausvyra
Kraskalo algoritmas
Monte-Karlo metodas
Kaip supakuoti standžiau?
Revoliucija mazgų teorijoje
Paslaptingi Markovo procesai
Diagramos pakeitusios pasaulį
Matematika prieš eismo spūstis
Klasikinės neišsprendžiamos geometrinės konstrukcijos
Kita skaičiavimo metodų istorijos pusė
Matematikos pradžia Lietuvoje
Išmatavimų triauškintojas
Kokiu greičiu skriejame?
Santykis ir proporcija
Harmoninės eilutės
Loterijų matematika
Smeilo paradoksas
Landau nuslopimas
Kvadratinė lygtis
Krafordo premija
Ferma taškas
Vartiklis